The Triangle and Its Properties Exercise 6.5 NCERT Solution for Class 7 Maths Chapter 6
The Triangle and Its Properties Exercise 6.1
The Triangle and Its Properties Exercise 6.2
The Triangle and Its Properties Exercise 6.3
The Triangle and Its Properties Exercise 6.4
Exercise 6.5
Q.1:- PQR is a triangle, right-angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
Solution 1:-
Given :- PQ = 10 cm; PR = 24 cm
For finding QR :- we need to use Pythagoras theorem
Lets QR = x cm;
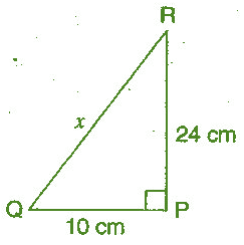
In the Right Angle Triangle RPQ,
(Hypotenuse)² = (Base)² + (Perpendicular)² [ by using the Pythagoras theorem]
x² = (10)² + (24)²
⇒ x² = 100 + 576
⇒ x² = 676
⇒ x = √676
⇒ x = 26
Hence, The length of QR = 26 cm.
Q.2:- ABC is a triangle, right-angled at C. If AB = 25 cm and AC = 7 cm, find BC.
Solution 2:-
Given :- AB = 25 cm; AC = 7 cm.
For finding BC :- we need to use Pythagoras theorem
Lets, BC = x cm
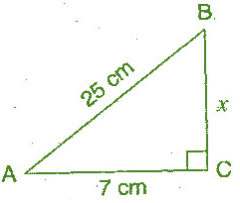
In the Right Angle Triangle ACB,
(Hypotenuse)² = (Base)² + (Perpendicular)² [ by using the Pythagoras theorem]
(25)² = (7)² + (x)²
⇒ x² = (25)² – (7)²
⇒ x² = 625 – 49
⇒ x = √576
⇒ x = 24
Hence, The length of BC = 24 cm.
Q.3 :- A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.

Solution 3:-
Given:- AC = 15 m, AB = 12 m, CB = a ;
Lets, the distance of the foot of the ladder from the wall = a meter
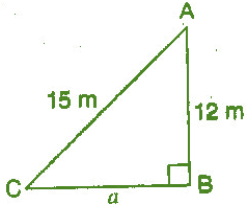
In the Right Angle Triangle CBA,
(Hypotenuse)² = (Base)² + (Perpendicular)² [ by using the Pythagoras theorem]
(15)² = (a)² + (12)²
⇒ a² = (15)² – (12)²
⇒ a² = 225 – 144
⇒ a = √81
⇒ a = 9
Hence, The length of CB = 9 m.
So, the distance of the foot of the ladder from the wall = 9 meter.
Q.4:- Which of the following can be the sides of a right triangle?
(i) 2.5cm, 6.5cm, 6cm.
(ii) 2cm, 2cm, 5cm.
(iii) 1.5cm, 2cm, 2.5cm.
In the case of right-angled triangles, identify the right angles.
Solution 4 (i):-
Given:- AC = 6.5 cm, AB = 6 cm, CB = 2.5 cm ;
For check :- Which can be the sides of a right triangle?
Using the Pythagoras theorem:-
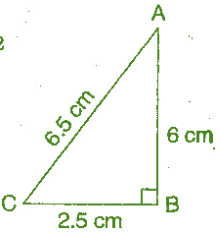
(Hypotenuse)² = (Base)² + (Perpendicular)²
(6.5)² = (2.5)² + (6)²
L.H.S = 6.5 x 6.5 = 42.25;
R.H.S = 2.5 x 2.5 + 6 x 6 = 6.25 + 36 = 42.25 ;
Since, L.H.S = R.H.S
Therefore, the given triangle right angle and given sides are of the right angled triangle.
Right angle lies on the opposite to the greater side 6.5 cm, which is at B.
Solution 4(ii):-
Given:- AC = 2 cm, 2 cm, 5 cm ;
For check :- Which can be the sides of a right triangle?
Using the Pythagoras theorem:-
(Hypotenuse)² = (Base)² + (Perpendicular)²
(2)² = (2)² + (5)²
L.H.S = 2 x 2 = 4;
R.H.S = 2 x 2 + 5 x 5 = 4 + 25 = 29 ;
Since, L.H.S ≠ R.H.S
Therefore, the given triangle are not right angle and given sides are not of the right angled triangle.
Solution 4(iii):-
Given:- AC = 2 cm, 2 cm, 5 cm ;
For check :- Which can be the sides of a right triangle?
Using the Pythagoras theorem:-
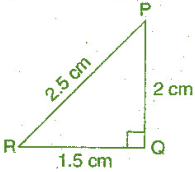
(Hypotenuse)² = (Base)² + (Perpendicular)²
(2.5)² = (1.5)² + (2)²
L.H.S = 2.5 x 2.5 = 6.25;
R.H.S = 1.5 x 1.5 + 2 x 2 = 2.25 + 4 = 6.25 ;
Since, L.H.S = R.H.S
Therefore, the given triangle right angle and given sides are of the right angled triangle.
Right angle lies on the opposite to the greater side 2.5 cm, which is at Q.
Q.5 :- A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
Solution 5:-
Q.6:- Angles Q and R of a ∆PQR are 25º and 65º.
Write which of the following is true:
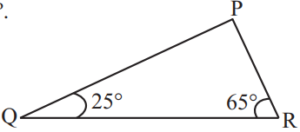
(i) PQ2 + QR2 = RP2
(ii) PQ2 + RP2 = QR2
(iii) RP2 + QR2 = PQ2
Q.7:- Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.
Solution 7:-
Q.8:- The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
Solution 8:-

