Ratio and Proportion Class 6 Ex. 12.1
Ratio and Proportion, Ncert Class 6, Chapter 12, Exercise 12.1 Math Free Solution.
Exercise 12.1
Question 1 :- There are 20 girl and 15 boy in a class.
(a) What’s the ratio of number of girls; to the number of boys?
(b) What’s the ratio of number of girls; to the total-number of students; in the class?
Solution 1:-
(a) Number of girls = 20
Number of boys = 15
Total number of students = 20 + 15 = 35
So, the ratio of the number of girls to the number of boys = 20/15 = 4/3;
Thus, the required ratio is 4 : 3.
(b) Ratio of the number of girls to the number of students = 20/35 = 4/7;
Therefore, a 4 : 7 ratio is needed.
Question 2 :- Out of 30-student in a class, 6-like football, 12-like cricket and remaining like tennis. Find the ratio of
(a) Number of student-liking football; to number of students liking tennis.
(b) Number of student-liking cricket; to total number of students.
Solution 2:-
Number of students in a class as a whole = 30;
Number of students liking football = 6
Number of students liking cricket = 12
Number of students liking tennis = 30 – (6 + 12) = 30 – 18 = 12
(a) Ratio of the number of the students liking football to number of students liking tennis = 6/12 = 1/2;
The necessary ratio is therefore 1 : 2.
(b) Ratio of the number of students liking cricket to total number of students = 12/30 = 2/5;
The necessary ratio is therefore 2 : 5.
Question 3 :- See the figures and find the ratio of :
(а) Number of triangle; to the number of circles; inside the rectangle.
(b) Number-of-square; to all the figures; inside the rectangle.
(c) Number of circle; to all the figures; inside the rectangle.
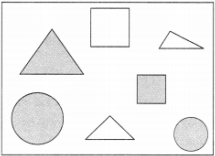
Solution 3:-
(a) Number of triangles 3
Number of circles = 2
Since, the ratio of number of triangles to the number of circles = 3/2;
Therefore, a 3 : 2 ratio is needed.
(b) Number of squares = 2
Number of all figures = 7
Since, the ratio of number of squares to the number of all the figures in the rectangle = 2/7;
Therefore, a 2 : 7 ratio is needed.
(c) Number of circles = 2
Number of all figures = 7
Since, the ratio of number of squares to the number of all the figures in the rectangle = 2/7;
Therefore, a 2 : 7 ratio is needed.
Question 4 :- Distance-travelled by Hamid and Akhtar; in an-hour; are 9-km and 12-km. Find the ratio of speed of Hamid to the speed of Akhtar.
Solution 4:-
Distance travelled by Hamid = 9 km;
Distance travelled by Akhtar = 12 km;
So, the-speed of Hamid = 9 km per hour;
So the-speed of Akhtar = 12 km per hour;
Since, the ratio of the speed of Hamid to the speed of Speed of Akhtar = 9/12 = 3/4;
Therefore, a 3 : 4 ratio is needed.
Question 5 :- Fill in the following-blank :
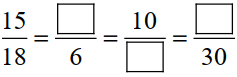[Are these equivalent ratios?]
Solution 5:-
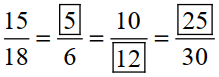
Yes, these are equivalent ratios.
Question 6 :- Find the-ratio; of the-following :
(a) 81 to 108
(b) 98 to 63
(c) 33 km to 121 km
(d) 30 minutes to 45 minutes
Solution 6:-
(a) 81/108 = (81/27)/(108/27) = 3/4; [ Since, H.C.F of 81 and 108 = 27 ]
So, the ratio of 81/108 = 3 : 4.
(b) 98/63 = (98/7)/(63/7) = 14/9; [ Since, H.C.F of 98 and 63 = 7 ]
So, the ratio of 98/63 = 14 : 9.
(c) 33/121 = (33/11)/(121/11) = 3/11; [ Since, H.C.F of 33 and 121 = 11 ]
So, the ratio of 33/121 = 3 : 4.
(d) 30/45 = (30/15)/(45/15) = 2/3; [ Since, H.C.F of 30 and 45 = 15 ]
So, the ratio of 30/45 = 2 : 3.
Question 7 :- Find the-ratio; of the-following :
(a) 30 minutes to 1.5 hours
(b) 40 cm to 1.5 m
(c) 55 paise to ₹ 1
(d) 500 mL to 2 litres
Solution 7:-
(a) 30 minutes to 1.5 hours
Since, 1 hour = 60 minutes
So, 1.5 hours = 60 x 1.5 minutes = 90 minutes
The ratio of 30 minutes to 1.5 hours = 30/90 = 1/3 = 1 : 3.
(b) 40 cm to 1.5 m
Since, 1 m = 100 cm
So, 1.5 m = 1.5 x 100 cm = 150 cm.
The ratio of 40 cm to 1.5 m = 40/150 = 4/15 = 4 : 15.
(c) 55 paise to ₹ 1
Since, ₹1 = 100 paise
So, the ratio of 55 paise to ₹ 1 = 55/100 = 11/20 = 11 : 20.
(d) 500 mL to 2 litres
Since, 1 litre = 1000 mL
So, 2 litres = 2 x 1000 mL = 2000 mL
The ratio of 500 mL to 2 litres = 500/2000 = 1/4 = 1 : 4.
Question 8 :- In a-year, Seema earns ₹1,50,000; and saves ₹50,000. Find; the-ratio of
(a) Money that Seema-earns to the money she-saves.
(b) Money that she-saves to the money she-spends.
Solution 8:-
(a) The money earned by Seema is = ₹ 1,50,000
Money saved by her = ₹ 50,000
The money spent by Seema is = ₹ 1,50,000 – ₹ 50,000 = ₹ 1,00,000
Since, the ratio of money earned by Seema to the money saved by her = 1,50,000/50,000;
3/1 = 3 : 1.
(b) Money earned by Seema = ₹ 1,50,000
Money saved by her = ₹ 50,000
Money spent by Seema is = ₹ 1,50,000 – ₹ 50,000 = ₹ 1,00,000
Since, the ratio of money saves by Seema to the money spends by her = 50,000/1,00,000;
1/2 = 1 : 2.
Question 9 :- There are 102-teacher in a-school of 3300-students. Find the ratio; of the number of teachers to the number-of-students.
Solution 9:-
Number of teachers = 102
Number of students = 3300
Since, the ratio of number of teachers to the number of students = 102/3300;
= (102/6)/(3300/6) = 17/550 = 17 : 550.
Question 10 :- In a-college; out of 4320-students, 2300-girls, find the ratio; of :
(а) Number of girls; to the total-number of students.
(b) Number of boys; to the number of girls.
(c) Number of boys; to the total-number of students.
Solution 10:-
Total number of students = 4320
Total number of girls = 2300
So, the total number of boys = 4320 – 2300 = 2020
(a) The ratio; of number-of-girl; to the total number-of-students; =
= 2300/4320 = (2300/20) / (4320/20) =115/216 = 115 : 216. [Since the H.C.F = 20]
(b) The ratio of Number-of-boy; to the number-of-girl; =
= 2020/2300 = (2020/20) / (2300/20) =101/115 = 101 : 115. [Since the H.C.F = 20]
(c) The ratio of Number-of-boy; to the total number-of-students; =
= 2020/4320 = (2020/20) / (4320/20) =101/115 = 101 : 216. [Since the H.C.F = 20]
Question 11 :- Out of 1800-students in a school, 750-opted basketball, 800-opted cricket; and remaining opted-table-tennis. If a student can opt only one-game, find the ratio of
(а) Number of students; who opted basketball; to the number of students who opted table-tennis.
(b) Number of students; who opted-cricket; to the number of students opting-basketball.
(c) Number of students; who opted basketball; to the total number of students.
Solution 11:-
Total number of students = 1800
Number of students opting basketball = 750
The number of students; who opted cricket = 800;
Number of remaining students who opted table tennis = 1800 – (750 + 800)
= 1800 – 1550 = 250
(а) The ratio of number of students; opted-basketball to the number of students; opted table-tennis =
= 750/250 = 3 = 3 : 1.
(b) The ratio of the students; opted-cricket to the number of students opting-basketball; =
= 800/750 = 16/15 = 16 : 15.
(c) The ratio of number of students; opted-basketball to the total-number-of-students; =
= 750/1800 = 5/12 = 5 : 12.
Question 12 :- Cost of a dozen-pens; ₹180 and cost of 8 ball pens; ₹56. Find the-ratio of the cost of a-pen to the cost of a ball-pen.
Solution 12:-
Since, the cost of 1, dozen(12) pens = ₹180
So, the cost of 1 pen = ₹180/12 = ₹15
Since, the cost of 8 ball pens = ₹56
So, the cost of 1 ball pen = ₹ 56/8 = ₹ 7
Now, for the ratio of cost of 1 pen to cost of 1 ball pen = 15/7;
Thus, required ratio is 15 : 7.
Question 13 :- Consider the-statement : Ratio of breadth and length of a hall; 2 : 5. Complete the following-table; that shows some possible-breadths and lengths of the hall.
Solution 13:-
Question 14 :- Divide 20-pen between Sheela and Sangeeta in the ratio 3 : 2.
Solution 14:- Ratio between Sheela and Sangeeta = 3 : 2;
Total of these ratio = 3 + 2 = 5;
Total number of pen = 20
So, Sheela’s share = (3/5) x 20 = 3 x 4 = 12 pens;
Shares owned by Sangeeta = (2/5) x 20 = 2 x 4 = 8 pens;
As a result, Sheela receives 12 pens and Sangeeta receives 8 pens.
Question 15 :- Mother wants to divide ₹36 between her daughters Shreya and Bhoomika in the ratio of their ages. If age of Shreya; 15-years and age of Bhoomika; 12-years, find how much Shreya and Bhoomika will get?
Solution 15:-
Total money that will be divide between Shereya and Bhoomika = ₹36;
Age of Shreya = 15 years;
Age of Bhoomika = 12 years;
Total of these age = 15 + 12 = 27;
Shreya’s share of money = (15/27) x 36 = ₹20
Bhoomika’s share of money = (12/27) x 36 = ₹16
Question 16 :- Present age of father; 42-years and that of his son; 14-years. Find the-ratio of
(a) Present-age of father to the present-age of son;
(b) Age of the father to the age of son, when son was 12-years-old;
(c) Age of father; after 10-years to the age of son after 10-years;
(d) Age of father to the age of son; when father was 30-years-old;
Solution 16:-
Present age of father = 42 years;
Son’s age at the present time = 14 years;
(a) Ratio of present age of father to the present age of son = 42/14 = 3/1 = 3 : 1.
(b) When son was 12 years old;
age of the father = 42 – 2 = 40 years;
Ratio between the father’s and son’s ages = 40/12 = 10/3 = 10 : 3.
(c) Father’s age after 10 years = 42 + 10 = 52 years
Son age after 10 years = 14 + 10 = 24 years
The ratio of father’s age after 10 years to the age of son after 10 years = 52/24 = 13/6 = 13 : 6.
(d) When Father’s age 30 years old;
Son’s age = 14 – 12 = 2 years;
The ratio of father’s age to the age of son when father was 30 years old = 30/2 = 15/1 = 15 : 1.
Chapter 12 Ratio and Proportion Class 6 Exercise. 12.1 for Free.