Ratio and Proportion Class 6 Ex. 12.2
Ratio and Proportion, Ncert Class 6, Chapter 12, Exercise 12.2 Math Free Solution.
Exercise 12.2
Question 1 :- Determine, if the following are in proportion.
(a) 15, 45, 40, 120
(b) 33, 121, 9, 96
(c) 24, 28, 36, 48
(d) 32, 48, 70, 210
(e) 4, 6, 8, 12
(f) 33, 44, 75, 100
Solution 1:-
(a)
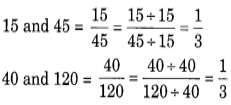
Since, 15 : 45 : : 40 : 120
So, 15, 45, 40 and 120 are in proportion.
(b)
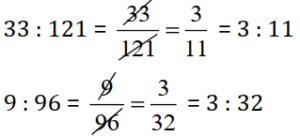
Since, 33 : 121 not equal to 9 : 96
So, 33, 121, 9, and 96 not in proportion.
(c)
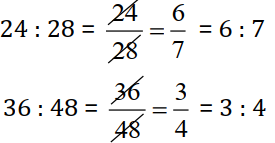
Since, 24 : 48 not equal to 36 : 48
So, 24, 28, 36, and 48 not in proportion.
(d)
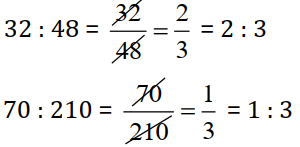
Since, 32 : 48 not equal to 70 : 210
So, 32, 48, 70, and 210 not in proportion.
(e)
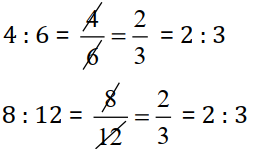
Since, 4 : 6 : : 8 : 12
So, 4, 6, 8 and 12 are in proportion.
(f)
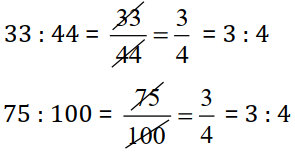
Since, 33 : 44 : : 75 : 100
So, 33, 44, 75 and 100 are in proportion.
Question 2 :- Write True (T) or False (F) against each of the following statements:
(a). 16 : 24 : : 20 : 30;
(b). 21 : 6 : : 35 : 10;
(c). 12 : 18 : : 28 : 12;
(d). 8 : 9 : : 24 : 27;
(e). 5.2 : 3.9 : : 3 : 4;
(f). 0.9 : 0.36 : : 10 : 4;
Solution 2:-
(a). 16 : 24 : : 20 : 30;
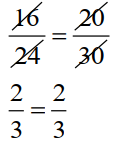
Product of the external terms = 16 x 30 = 480
Product of the internal terms = 24 x 20 = 480
So, The given statement (a) is True.
(b). 21 : 6 : : 35 : 10;
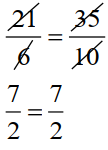
Product of the external terms = 21 x 10 = 210
Product of the internal terms = 6 x 35 = 210
So, The given statement (b) is True.
(c). 12 : 18 : : 28 : 12;
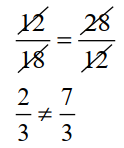
Product of the external terms = 12 x 12 = 144
Product of the internal terms = 18 x 28 = 504
Since 144 ≠ 504 or 12 : 18 not equals to 28 : 12
So, The given statement (c) is False.
(d). 8 : 9 : : 24 : 27;
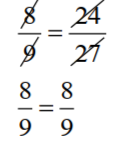
The product of the external terms = 8 x 27 = 216
The product of the internal terms = 9 x 24 = 216
So, the given statement (d) is True.
(e). 5.2 : 3.9 : : 3 : 4;
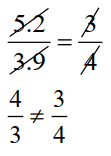
Product of the extreme terms = 5.2 x 4 = 20.8
Product of the middle terms = 3.9 x 3 = 11.7
Since, 20.8 ≠ 11.7 or 5.2 : 3.9 not equals to 3 : 4
So, the given statement (e) is False.
(f). 0.9 : 0.36 : : 10 : 4;
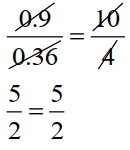
Product of the external terms = 0.9 x 4 = 3.6
Product of the internal terms = 0.36 x 10 = 3.6
Since, 3.6 = 3.6 or 5.2 : 3.9 not equals to 3 : 4
So, the given statement (f) is True.
Question 3 :- Are the following statements true?
(a). 40 persons : 200 persons = ₹15 : ₹75;
(b). 7.5 litres : 15 litres = 5 kg : 10 kg;
(c). 99 kg : 45 kg = ₹ 44 : ₹ 20;
(d). 32 m : 64 m = 6 sec : 12 sec;
(e). 45 km : 60 km = 12 hours : 15 hours;
Solution 3:-
(a). 40 persons : 200 persons =
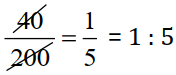
₹15 : ₹75 =
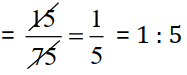
Since, 40 persons : 200 persons = ₹15 : ₹75
So, the statement (a) is True.
(b) 7.5 litres : 15 litres =
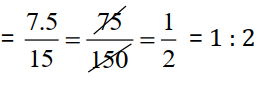
5kg : 10kg =
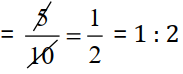
Since, 7.5 litres : 15 litres = 5 kg : 10 kg
So, the statement (b) is True.
(c) 99 kg : 45 kg =
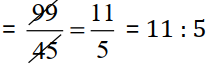
₹ 44 : ₹ 20 =
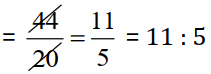
Since, ratios are equal :- 99 kg : 45 kg = ₹ 44 : ₹ 20;
So, the statement (c) is True.
(d) 32 m : 64 m =
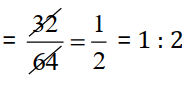
6 sec : 12 sec =
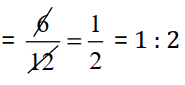
Since, ratios are equal :- 32 m : 64 m = 6 sec : 12 sec
So, the statement (d) is True.
(e). 45 km : 60 km = 12 hours : 15 hours;
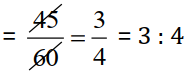
12 hours : 15 hours =
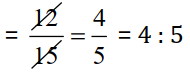
Since, 45 km : 60 km = 12 hours : 15 hours
So, the statement (e) is not true.
Question 4 :- Determine; if the following ratio form a proportion. Also, write the middle-terms and extreme-terms; where the ratios form a proportion.
(a) 25cm : 1m and ₹40 : ₹160
(b) 39-litres : 65-litres and 6-bottles : 10-bottles;
(c) 2kg : 80kg and 25g : 625g
(d) 200mL : 2.5 litres and ₹4 : ₹50
Solution 4:-
(a) 25cm : 1m = 25cm : 100cm ; [ Since, 1 m = 100 cm ]
25/100 = 1/4 = 1 : 4; and
| ₹40 : ₹160 = 40/160 = 1/4 = 1 : 4;
So, the given ratios are in proportion.
.Extreme-terms are 25 cm and ₹ 160;
Middle terms are 1 m and ₹40.
(b) 39 litres : 65 litres =
39/65 = (39/13)/(65/13) = 3/5 = 3 : 5; and
6 bottle : 10 bottle = 6/10 = 3/5 = 3 : 5;
So, the given ratios are in proportion.
Extreme terms are 39 litres and 10 bottle.
Middle terms are 65 litres and 6 bottle.
(c) 2 kg : 80 kg =
2/80 = 1/40 = 1 : 40; and
25g : 625g = 25/625 = 1/5 = 1 : 5;
Since, the ratio are not equal
So, the given ratios are not in proportion.
Extreme terms are 2 kg and 625 g.
Middle terms are 80 kg and 25 g.
(d) 200 ml : 2.5 litres = 200ml : 2500 ml [ Since, 1 litres = 1000 ml ]
200/2500 = 2/25 = 2 : 25; and
₹ 4 : ₹ 50 = 4/50 = 2/25 = 2 : 25;
Since, the ratio are equals
So, the given ratios are in proportion.
Extreme terms are 200 ml and ₹ 50.
Middle terms are 2.5 litres and ₹ 4.
Chapter 12 Ratio and Proportion Class 6 Exercise. 12.2 for Free.
