Simple Equations Ncert Solution for Class 7 Maths Chapter 4 Exercise 4.1

Simple Equations Class 7 Ex. 4.1;

Simple Equations for Class 7, Chapter 4 Maths NCERT Solution ;

 

Exercise 4.1

Question 1:- Complete the given column of the table:

Solution 1:-

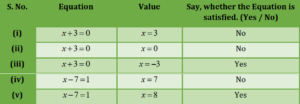
Question 2 :- Check, whether the-value, given in the brackets is a solution to the given equation or not:
(a) n + 5 = 19; (n = 1).
(b) 7n + 5 = 19; (n = -2).
(c) 7n + 5 = 19; (n = 2).
(d) 4p – 3 = 13; (p = 1).
(e) 4p – 3 = 13; (p = -4).
(f) 4p – 3 = 13; (p = 0).
Solution 2:-
(a) n + 5 = 19 (n = 1)
Put, n = 1 in L.H.S
1 + 5 = 6 ≠ 19 (R.H.S)
Since L.H.S ≠ R.H.S
So, (n = 1), is not the solution of the given equation.

(b) 7n + 5 = 19; (n = -2)
Put, n = – 2 in L.H.S
7 × (-2) + 5 = -14 + 5 = -9 ≠ 19 (R.H.S)
Since, L.H.S ≠ R.H.S
SO, (n = -2), is not the solution of the given equation.

(c) 7n+ 5 = 19; (n = 2)
Put, n = 2 in L.H.S
7 ×(2) + 5 = 14 + 5 = 19 = 19 (R.H.S)
Since, L.H.S = R.H.S
So, (n = 2), is the solution of the given equation.

(d) 4p – 3 = 13; (p = 1)
Put, p = 1 in L.H.S
4 ×(1) – 3 = 4 – 3 = 1 ≠ 13 (R.H.S)
Since, L.H.S ≠ R.H.S
So, (p = 1), is not the solution of the given equation.

(e) 4p – 3 = 13; (p = -4)
Put, p = -4 in L.H.S
4 ×(-4) – 3 = -16 – 3 = -19 ≠ 13 (R.H.S)
Since, L.H.S ≠ R.H.S
So, (p = -4), is not the solution of the given equation.

(f) 4p – 3 = 13; (p = 0)
Put p = 0 in L.H.S
4 × (0) – 3 = 0 – 3 = -3 ≠ 13 (R.H.S)
Since, L.H.S ≠ R.H.S
So, (p = 0), is not the solution of the given equation.

Simple Equations Chapter 4 Ex. 4.1 For Class 7

Question 3:- Solve, the following equations, by trial and error method:
(i) 5p + 2 = 17
(ii) 3m – 14 = 4

Solution 3:- 
(i) 5p + 2 = 17
For, p = 1, L.H.S
= 5 × 1 + 2 = 5 + 2 = 7 ≠ 17 (R.H.S)
For p = 2, LHS = 5 × 2 + 2
= 10 + 2 = 12 ≠ 17 (R.H.S)
For p = 3, LHS = 5 × 3 + 2
= 15 + 2 = 17 = 17 (R.H.S)
Since, p = 3 satisfies the above equation, p = 3 is the necessary solution.

(ii) 3m – 14 = 4
For m = 1, L.H.S = 3 × 1 – 14
= 3 – 14 = -11 ≠ 4 (R.H.S)
For m = 2, L.H.S = 3 × 2 – 14 = 6 – 14
= -8 ≠ 4 (R.H.S)
For m = 3, L.H.S = 3 × 3 – 14 = 9 – 14
= -5 ≠ 4 (R.H.S)
Form m = 4, L.H.S = 3 × 4 – 14
= 12 – 14 = -2 ≠ 4 (R.H.S)
For m = 5, L.H.S = 3 × 5 – 14
= 15 – 14 = -1 ≠ 4 (R.H.S)
For m = 6, L.H.S = 3 × 6 – 14
= 18 – 14 = 4 (=) 4 (R.H.S) .
Considering that for m = 6, the preceding equation is satisfied.
Therefore, the necessary solution is m = 6.

Simple Equations Chapter 4 Ex. 4.1 For Class 7

Question 4 :- Write equations for the following statements:
(i) The sum of numbers, x and 4 is 9.
(ii) 2 subtracted from y is 8.
(iii) Ten times a is 70.
(iv) The number b, divided by 5 gives 6.
(v) Three-fourth of t is 15.
(vi) Seven times m, plus 7 gets you 77.
(vii) One-fourth of a number x, minus 4 gives 4.
(viii) If you take away 6, from 6 times y, you get 60.
(ix) If you add 3, to one-third of z, you get 30.
Solution 4:-

(i) x+4 = 9

(ii) y-2 = 8

(iii) 10a = 70

(iv) b/5 = 6

(v) (3/4) (t) = 15

(vi) 7m + 7 = 77

(vii) (1/4)(x) – 4 = 4

(viii) 6y-6 = 60

(viii) (1/3) (z) + 3 = 30

Simple Equations Chapter 4 Ex. 4.1

Question 5 :- Write the following equations in statement forms.

Solution 5:-

degree.

Solutions 6:- (i) 5m+7 = 37.

(ii) Let, Laxmi’s age be ‘y’ years.
Since, Laxmi’s father’s age = 3y + 4
However, the age of Laxmi’s father is 49.
Thus the required equation is 3y + 4 = 49

(iii) Let the lowest score be L.
Since, the highest score = 2L + 7
But 87 receives the highest score.
Thus, the required equation is 2L + 7 = 87

(iv) Let, each base angle be ‘b’ degrees.
Since, Vertex angle of the triangle = 2b
A triangle’s total angles equal 180°.
Hence, the required equation is b + b + 2b = 180° or 4b = 180°

---

Simple Equations Chapter 4 Math Solutions for NCERT

---

Simple Equations

Simple Equations