Playing With Numbers Class 6 Ex. 3.5
Ncert Class 6 Math Free Solution.
Exercise 3.5
Question 1:- Here are two different factor trees for 60. Write the missing numbers.
( a ) 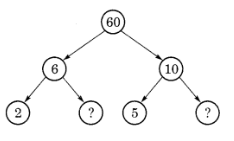 ( b )
( b ) 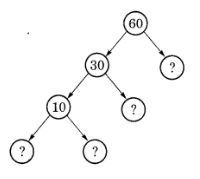
Solution 1:-
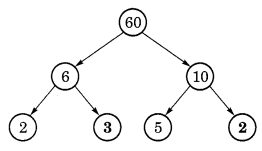
(a) Here, 6 = 2 x missing number
So, Missing number = 6/2 = 3
Similarly, 10 = 5 x missing number
So, Missing number = 10 ÷ 5 = 2
Hence, the missing numbers are 3 and 2.
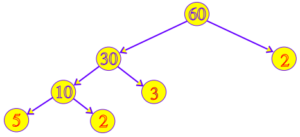
(b) 60 = 30 x missing number
So, missing number = 60 ÷ 30 = 2
30 = 10 x missing number
So, missing number = 30 ÷ 10 = 3
10 = missing number x missing number
So, missing number = 2 or 5 and missing number = 5 or 2
Hence, the missing numbers are 2, 3, 2, 5.
Question 2 :- Which factors are not included in the prime factorisation of a composite number?
Solution 2:-
A composite number’s prime factorization excludes both 1 and the number itself.
Question 3 :- Write the greatest 4-digit number and express it in terms of its prime factors.
Solution 3:-
The greatest 4-digit number = 9999
So, the prime factors of 9999 = 3 x 3 x 11 x 101.
Question 4 :-Write the smallest 5-digit number and express it in the form of its prime factors.
Solution 4:-
The smallest 5-digit number = 10000
So, the required prime factors: 10000 = 2 x 2 x 2 x 2 x 5 x 5 x 5 x 5.
Question 5 :- Find all the prime factors of 1729 and arrange them in ascending order. Now state the relations, if any, between the two consecutive prime factors.
Solution 5 :-
The prime factors of 1729 = 7 X 13 X 19.
Here are , 13 – 7 = 6 and 19 – 13 = 6
So, the difference between two consecutive prime factors is 6.
Question 6 :- The product of three consecutive numbers is always divisible by 6. Verify this statement with the help of some examples.
Solution 6:-
Example 1:
Lets take three consecutive numbers 20, 21 and 22.
Here 20 is divisible by 2 and 21 is divisible by 3.
So, the product 20 x 21 x 22 = 9240 is divisible by 6.
Example 2:
Lets take three consecutive numbers 2; 3 and 4.
Here 2 is divisible by 2 and 3 is divisible by 3.
Therefore, the product 2 x 3 x 4 = 24 is divisible by 6.
Example 3:
Take three consecutive numbers 4, 5 and 6.
Here, 4 is divisible by 2 and 6 is divisible by 3.
Therefore, the product 4 x 5 x 6 = 120 which is divisible by 6.
Question 7 :-The sum of two consecutive odd numbers is divisible by 4. Verify this statement with the help of some examples.
Solution 7:-
Example 1:
Lets take two consecutive odd numbers 3 and 5.
Sum = 3 + 5 = 8
Here, the number formed by last two digits is 8 which is divisible by 4.
Hence, the sum of numbers 3 and 5 i.e. 8 is divisible by 4.
Example 2:
Let us take two consecutive odd numbers 5 and 7.
Sum = 5 + 7 = 12
Here, the number formed by last two digits is 12 which is divisible by 4.
Example 3:
Let us take two consecutive odd numbers 7 and 9.
Sum = 7 + 9 = 16
Here, the number formed by the last two digits is 16 which is divisible by 4.
Question 8 :- In which of the following expressions, prime factorisation has been done?
(a) 24 = 2 x 3 x 4
(b) 56 = 7 x 2 x 2 x 2
(c) 70 = 2 x 5 x 7
(d) 54 = 2 x 3 x 9.
Solution 8:-
(a) 24 = 2 X 3 X 4
Here, 4 is not a prime number.
So, 24 = 2 X 3 X 4 is not a prime factorisation.
(b) 56 = 7 X 2 X 2 X 2
Here, all factors are prime numbers
So, 56 = 7 X 2 X 2 X 2 is a prime factorisation.
(c) 70 = 2 X 5 X 7
Here, all factors are prime numbers.
So, 70 = 2 X 5 X 7 is a prime factorisation.
(d) 54 = 2 x 3 x 9
Here, 9 is not a prime number.
So, 54 = 2 X 3 X 9 is not a prime factorisation.
Question 9 :- 18 is divisible by both 2 and 3. It is also divisible by 2 x 3 = 6. Similarly, a number is divisible by both 4 and 6. Can we say that the number must also be divisible by 4 x 6 = 24? If not, give an example to justify your answer.
Solution 9:-
The given two numbers are not co-prime. So, It is not required that a number that can be divided by 4 and 6 also can be divided by their product, which is 24 in this case.
Example1:- No. Number 12 is divisible by 4 and 6; but it is not necessary, divisible by 6X4 = 24 .
Example 2:- 36 and 60 are divisible by 4, both 4 and 6 but not by 24.
Question 10 :- I am the smallest number, having four different prime factors. Can you find me?
Solution 10:-
The smallest four prime numbers are 2, 3, 5, and 7, as is well known.
Hence, the required number = 2 x 3 x 5 x 7 = 210.
Playing With Numbers Class 6 Exercise. 3.5 for Free
