Playing With Numbers Class 6 Ex. 3.7
Ncert Class 6 Math Free Solution.
Exercise 3.7
Question 1 :- Renu purchases two bags of fertiliser of weights 75 kg and 69 kg. Find the maximum value of weight which can measure the weight of the fertiliser exact number of times.
Solution 1:-
For finding maximum value of weight, we have to find out H.C.F. of 75 and 69
The factor. of 75 = 3 X 5 X 5
Factor of 69 = 3 x 23
H.C.F = 3
The required maximum weight is therefore 3 kg.
Question 2 :- Three boys step off together from the same spot. Their steps measure 63 cm, 70 cm and 77 cm respectively. What is the minimum distance each should cover so that all can cover the distance in complete steps?
Solution 2:- For finding minimum distance, we have to find L.C.M of 63, 70 and 77.
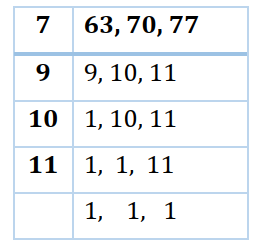
∴ LCM of 63, 70 and 77 = 7 x 9 x 10 x 11 = 6930
Therefore, 6930 cm is the required minimum distance.
Question 3 :- The length, breadth and height of a room are 825 cm, 675 cm and 450 cm respectively. Find the longest tape which can measure the three dimensions of the room exactly.
Solution 3:-
HCF of 825, 675 and 450
Factor of 825 = 3 x 5 x 5 x 11
Factor of 675 = 3 x 3 x 3 x 5 x 5
Factor of 450 = 2 x 3 x 3 x 5 x 5
Here, common factors are 3, 5, 5.
So, HCF of 825, 675 and 450 = 3 x 5 x 5 = 75
The required longest tape is therefore 75 cm.
Question 4 :- Determine the smallest 3-digit number which is exactly divisible by 6, 8 and 12.
Solution 4:-
The smallest 3-digit number = 100
LCM of 6, 8 and 12
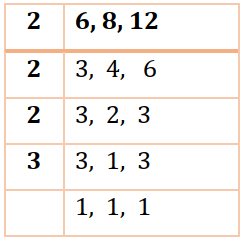
So, the LCM of 6, 8 and 12 = 2 x 2 x 2 x 3 = 24
Due to the fact that all multiples of 24 can be divided by 6, 8, and 12 numbers.
So, the smallest multiple of 24 in three digits will be just above100
(100 – 4) + 24 = 96 + 24 = 120
Hence, the required number is 120.
Question 5 :- Determine the greatest 3-digit number exactly divisible by 8, 10 and 12.
Solution 5:-
The L.C.M of 8, 10 and 12,
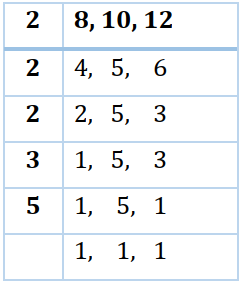
L.C.M of 8, 10 and 12 = 2 x 2 x 2 x 3 x 5 = 120
The greatest 3-digit number = 999

Hence, the required number is 999 – 39 = 960.
Question 6 :- The traffic lights at three different road crossings change after every 48 seconds, 72 seconds and 108 seconds respectively. If they change simultaneously at 7 a.m., at what time will they change simultaneously again?
Solution 6:-
To find the LCM of 48, 72 and 108,
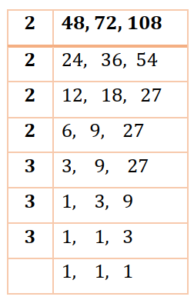
Since, LCM = 2 x 2 x 2 x 2 x 3 x 3 x 3= 432
As a result, the light will change simultaneously after 432 seconds.
As a result, the necessary time is 432 seconds, or 7 minutes and 12 seconds, or 7 minutes and 12 seconds after 7 a.m.
Question 7 :- Three tankers contain 403 litres, 434 litres and 465 litres of diesel respectively. Find the maximum capacity of a container that can measure the diesel of the three containers exact number of times.
Solution 7:-
The needed measure’s maximum capacity is equivalent to the HCF of 403, 434, and 465.
Prime factor. of 403, 434 and 465 are
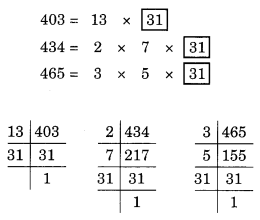
Common factor = 31.
The HCF of 403, 434, and 465 is therefore 31.
Therefore, the needed container’s maximum capacity is 31 liters.
Question 8 :- Find the least number which when divided by 6, 15 and 18 leave remainder 5 in each case.
Solution 8:-
The L.C.M of 6, 15 and 18,

L.C.M of 6, 15 and 18 = 2 x 3 x 3 x 5 = 90.
The least number 90 that is precisely divisible by 6, 15, and 18 in this case.
To get a remainder 5, the least number will be 90 + 5 = 95.
Hence, the required number is 95.
Question 9 :-Find the smallest 4-digit number which is divisible by 18, 24 and 32.
Solution 9:-
The smallest 4-digit number = 1000.
The L.C.M of 18, 24 and 32,
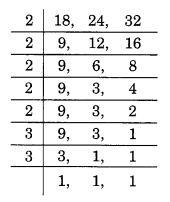
L.C.M = 2 x 2 x 2 x 2 x 2 x 3 x 3 = 288
The smallest number that is precisely divisible by 18, 24, and 32 is 288.
But it is not a 4-digit number.
So, the multiple of 288 just above 1000 is: 1000 – 136 + 288 = 1152.
Hence, the required number is 1152.
Question 10 :-Find the LCM of the following numbers:
(a) 9 and 4
(b) 12 and 5
(c) 6 and 5
(d) 15 and 4
Observe a common property in the obtained LCMs. Is LCM the product of two numbers in each case?
Solution 10:-
(a) The L.C.M of 9 and 4,
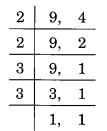
L.C.M = 2 x 2 x 3 x 3 = 36.
The product 9 x 4 = 36.
LCM of 9 and 4 hence equals product of 9 and 4.
(b) To find LCM of 12 and 5,

L.C.M = 2 x 2 x 3 x 5 = 60.
The product 12 x 5 = 60.
LCM of 12 and 5 hence equals product of 12 and 5.
(c) The L.C.M of 6 and 5,
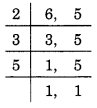
L.C.M = 2 x 3 x 5 = 30.
The product 6 x 5 = 30.
LCM of 6 and 5 hence equals product of 6 and 5.
(d) The LCM of 15 and 4,
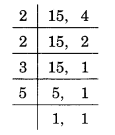
L.C.M = 2 x 2 x 3 x 5 = 60.
The product 15 x 4 = 60.
LCM of 15 and 4 hence equals product of 15 and 4.
Question 11 :- Find the LCM of the following numbers in which one number is the factor of the other.
(a) 5, 20
(b) 6, 18
(c) 12, 48
(d) 9, 45
What do you observe in the results obtained?
Solution 11:-
(a) The L.C.M of 5 and 20,

L.C.M = 2 x 2 x 5 = 20.
Hence, the L.C.M of 5 and 20 = 20.
(b) The L.C.M of 6 and 18,
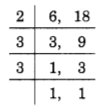
L.C.M = 2 x 3 x 3 = 18.
Hence, the LCM of 6 and 18 = 18.
(c) The L.C.M of 12 and 48,

LCM = 2 x 2 x 2 x 2 x 3 = 48.
Hence, the LCM of 12 and 48 = 48.
(d) The L.C.M of 9 and 45,
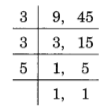
LCM = 3 x 3 x 5 = 45.
Hence, the LCM of 9 and 45 = 45.
From the above examples, we observe that the LCM of the two numbers, where one number is a factor of the other, is the greater number.
Playing With Numbers Class 6 Exercise. 3.7 for Free
