The Triangle and Its Properties NCERT Solution for Class 7 Maths Chapter 6 Exercise 6.3

The Triangle and Its Properties Exercise 6.3 NCERT Solution for Class 7 Maths Chapter 6

The Triangle and Its Properties Exercise 6.1
The Triangle and Its Properties Exercise 6.2
The Triangle and Its Properties Exercise 6.4
The Triangle and Its Properties Exercise 6.5

Exercise 6.3

Q.1 :- Find the value of the unknown x in the following diagrams: 

           

               

Solution 1:-

Q.1 :-  Find the values of the unknowns x and y in the following diagrams:

Solution 1:-  By The  Angle Sum Property Of A Triangle 

Formula:- The total measure of the three angles of a triangle is 180°.

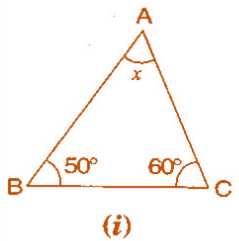
Solution 1.(i) :- In Triangle ABC, 
∠BAC + ∠ACB + ∠ABC = 180º,     [ By the angle sum property of triangle ]

x + 60º+ 50º = 180º,
x + 110º = 180º,
x = 180º – 110º,
x= 70º.

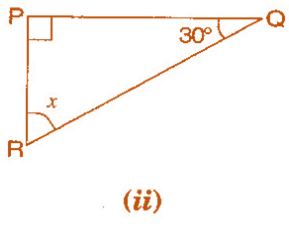
Solution 1.(ii) :- In Triangle PQR, 
∠PRQ + ∠PQR + ∠RPQ = 180º,     [ By the angle sum property of triangle ]

x + 30º+ 90º = 180º,
x + 120º = 180º,
x = 180º – 120º,
x= 60º.

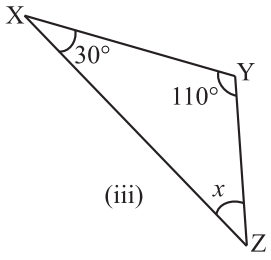
Solution 1.(iii) :- In Triangle XYZ, 
∠XZY + ∠XYZ + ∠ZXY = 180º,     [ By the angle sum property of triangle]

x + 110º+ 30º = 180º,
x + 140º = 180º,
x = 180º – 140º,
x= 40º.

Solution 1.(iv) :- In The Isosceles Triangle, 
∠1 + ∠2 + ∠3 = 180º,     [ By the angle sum property of triangle]

x + x+ 50º = 180º,
2x + 50º = 180º,
2x = 180º – 50º,
x = 130º/2 ,
x = 65º.

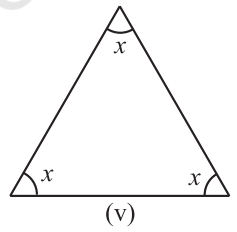
Solution 1.(v) :- In The Equilateral Triangle, 
∠1 + ∠2 + ∠3 = 180º,     [ By the angle sum property of triangle]

x + x+ x = 180º,
3x = 180º,
x = 180º/3 ,
x = 60º.

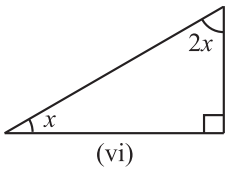
Solution 1.(vi) :- In The Given Right Angle Triangle, 
∠1 + ∠2 + ∠3 = 180º,     [ By the angle sum property of triangle]

x + 2x+ 90º = 180º,
3x + 90º = 180º,
3x = 180º – 90º,
x = 90º/3,
x = 30º.

Q.2:- Find the values of the unknowns x and y in the following diagrams: 

             

         

Solution 2:- 
  
Solution 2.(i) :- In The Given Triangle, 
x + 50º = 120º,     [ By the Exterior angle property of a triangle ]
x = 120º – 50º,
x = 70º

Now, For The Value of Y, using Angle sum property of a triangle,
x + y + 50º = 180º,
70º + y + 50º = 180º,
y + 120º = 180º,
y = 180º – 120º,
y = 60º.

Hence, x=70º and y=60º.

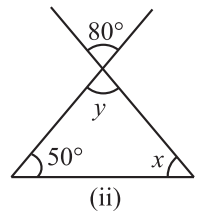
Solution 2.(ii) :- In The Given Triangle, 
y = 80º,     [ By the Vertically Opposite angle property of a triangle ]

Now, For The Value of X, using Angle sum property of a triangle,
x + y + 50º = 180º,
x + 80º + 50º = 180º,
x + 130º = 180º,
x = 180º – 130º,
x = 50º.

Hence, x=50º and y=80º.

Solution 2.(iii) :-In The Given Triangle, 
x = 50º + 60º,     [ By the Exterior angle property of a triangle ]
x = 110º ,

Now, For The Value of Y, using Angle sum property of a triangle,
y + 60º + 50º = 180º,
y + 110º = 180º,
y = 180º – 110º,
y = 70º.

Hence, x=110º and y=70º.

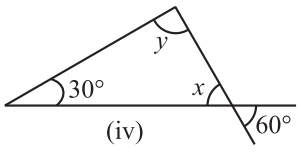
Solution 2.(iv) :-In The Given Triangle, 
x = 60º,                         [ By the Vertically Opposite angle property of a triangle ]

Now, For The Value of Y, using Angle sum property of a triangle,
x + y + 30º = 180º,
60º + y + 30º = 180º,
y + 90º = 180º,
y = 180º – 90º,
y = 90º.

Hence, x=60º and y=90º.

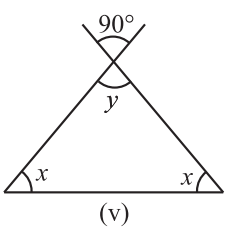
Solution 2.(v) :-In The Given Triangle, 
y = 90º,                    [ By the Vertically Opposite angle property of a triangle ]

Now, For The Value of X, using Angle sum property of a triangle,
x + x + y = 180º,
2x + 90º  = 180º,
2x = 180º – 90º,
2x = 90º,
x = 90º/2,
x = 45º.

Hence, x=45º and y=90º.

Solution 2.(vi) :- In The Given Triangle, 
x = y,                    [ By the Vertically Opposite angle property of a triangle ]

Now, For The Value of Y, using Angle sum property of a triangle,
x + x + y = 180º,
x + x + x  = 180º,
3x = 180º,
x = 180º/3,
x = 60º.

Hence, x=60º and y=60º.

---

NCERT Solutions for Class 7 Math, Chapter 6 – The Triangle and Its Properties, Exercise-6.3