Data Handling Class 7 Ex. 3.1;
New Ncert Solution for Class 7 Maths Chapter 3 Data Handling Free Solution;
Exercise 3.1
Question 1 :- Find the range, of heights of any ten-students of your class.
Solution 1:-
Let’s take the heights of 10 students are as follows:
Student 1 = 140 cm,
Student 2 = 141.5 cm,
Student 3 = 138 cm,
Student 4 = 150 cm,
Student 5 = 161 cm,
Student 6 = 138 cm,
Student 7 = 140.5 cm,
Student 8 = 135.5 cm,
Student 9 = 160 cm,
Student 10 = 158 cm
Now, the minimum height of student = 135.5 cm
The maximum height of student =161 cm
So, Range = Maximum height – Minimum height
= 161 cm – 135.5 cm = 25.5 cm
Hence, the required range = 25.5 cm.
Question-2:- Organize, the following marks in a class-assessment in a tabular-form.
4, 6, 7, 5, 3, 5, 4, 5, 2, 6, 2, 5, 1, 9, 6, 5, 8, 4, 6, 7
(i) Which number is the highest?
(ii) Which number is the lowest?
(iii) What is the range of the data?
(iv) Find the arithmetic mean.
Solution 2:-
Let’s make a frequency distribution table:
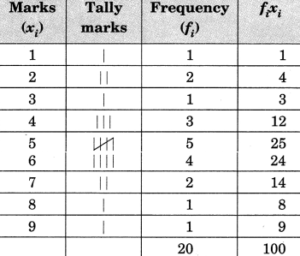
(i) Marks 9, is the highest marks.
(ii) Marks 1, is the lowest marks.
(iii) Range = Max. marks – Min. marks
= 9 – 1 = 8
(iv) Arithmetic mean = Σ(fixi)/Σ(fi)=100/20 = 5.
Question-3:- Find the mean of first five whole numbers.
Solution-3:-
The first 5-whole numbers are = 0, 1, 2, 3, 4
So, the mean of first five numbers = Sum of number/ total number
= (0+1+2+3+4)/5 = 10/5 = 2
Hence, the required mean = 2.
Question 4 :- A cricketer-scores, the following runs in eight innings are :
58, 76, 40, 35, 46, 45, 0, 100
Find the mean-score.
Solution 4:-
Total number of inning = 8
Following are the scores of the runs in 8 innings:
58, 76, 40, 35, 46, 45, 0, 100
So, Mean = Sum of all scores/Number of innings
= (58+76+40+35+46+45+0+100)/8 = 400/8 = 50
Hence, the required mean = 50.
Question 5 :- Following-table shows, the points of each-player scored in four-games:
| Player | Game 1 | Game 2 | Game 3 | Game 4 |
| A | 14 | 16 | 10 | 10 |
| B | 0 | 8 | 6 | 4 |
| C | 8 | 11 | Did not play | 13 |
Now answer the following questions:
(i) Find the mean to determine A’s average number of points scored per game.
(ii) To find, the mean-number of points per game for C, would you divide the total points by 3 or by 4 ? Why ?
(iii) B played in all the four games. How would you find the mean?
(iv) Who is the best performer?
Solution 5:-
(i)
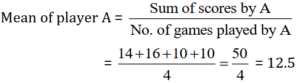
(ii) Since, player C did not play Game 3, he played only 3 games. So, the sum of all digit will be divided by 3.
(iii) Number of points scored by B, (in all the games) are
Game 1 = 0, Game 2 = 8, Game 3 = 6, Game 4 = 4
Average score = (0+8+6+4)/4 = 18/4 = 4.5
(iv) Mean score of player A = 12.5
Mean score of player B = 4.5
Mean score of player C = (8+11+13)/3 = 32/3 = 10.67
Clearly, A is the best performer.
Question 6 :- The marks, (out of 100) obtained by a group of students in a science-test are 85, 76, 90, 85, 39, 48, 56, 95, 81 and 75. Find the
(i) Highest and the lowest marks obtained by the students.
(ii) Range of the marks obtained.
(iii) Mean marks obtained by the group.
Solution 6:-
Marks obtained by the students are:
85, 76, 90, 85, 39, 48, 56, 95, 81 and 75
(i) Highest marks obtain by student = 95
Lowest marks obtain by the student = 39
(ii) Range of the marks = ( Highest-marks – Lowest-marks )
= 95 – 39 = 56
(iii)
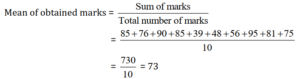
So, the mean-marks, obtain by the group = 73.
Question 7 :- The enrolment, in a-school during six-consecutive years was as follows:
1555, 1670, 1750, 2013, 2540, 2820
Find the mean, enrolment of the school for this period.
Solution 7:-
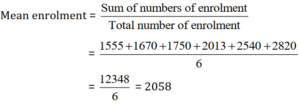
Thus, the required-mean = 2058.
Question 8 :- The rainfall (in mm) in a city on 7 days of a certain week was recorded as follows:
| Day | Rainfall (in mm) |
| Monday | 0.0 |
| Tuesday | 12.2 |
| Wednesday | 2.1 |
| Thursday | 0.0 |
| Friday | 20.5 |
| Saturday | 5.5 |
| Sunday | 1.0 |
(i) Find the range, of the rainfall in the above data.
(ii) Find the mean, rainfall for the week.
(iii) On how-many days was the rainfall less than the mean-rainfall?
Solution 8:-
(i) Since, maximum rainfall = 20.5 mm
Minimum rainfall = 0.0 mm
So, Range = Maximum rainfall – Minimum rainfall
= 20.5 mm – 0.0 mm = 20.5 mm
(ii) Mean rainfall = (0.0 + 12.2 + 2.1 + 0.0 + 20.5 + 5.5 + 1.0)/7 = (41.3) / 7 = 5.9 mm.
(iii) Total number of days on which the rainfall was less than the mean rainfall =
Monday, Wednesday, Thursday, Saturday, Sunday = 5 days.
Question 9 :- The heights of 10-girls were measured (in cm) and the results are as follows:
135, 150, 139, 128, 151, 132, 146, 149, 143, 141
(i) What is the height of the tallest-girl?
(ii) What is the height of the shortest girl?
(Hi) What is the range of the data?
(iv) What is the mean height of the girls?
(v) How many girls have heights more than the mean height?
Solution 9:-
(i) The height of the tallest-girl = 151 cm.
(ii) The height of the shortest-girl = 128 cm.
(iii) The range = Height of tallest-girl – Height of the shortest-girl
= 151 cm – 128 cm = 23 cm.
(iv) Mean of the height = (135+150+139+128+151+132+146+149+143+141)/10 = 1414/10 = 141.4 cm.
(v) Total number of girls having more height than the mean height
= 150, 151, 146, 149 and 143 = 5 girls.
